For many children, it seems that even if their calculation skills are up to speed, being presented with a word problem can cause them to freeze in confusion as they struggle to make sense of it.
For them, the issue is not doing the maths. It’s finding the maths to do.
The question on the right, for example, is deliberately nonsensical. When I showed it to some Year 6 children recently, I expected them to realise I was pulling their leg almost immediately. Yet it was a good 45-60 seconds before any of them realised that it was ridiculous and couldn’t be solved*.
I wonder why? I have a theory…

I suspect that children read a word problem without a strategy, hoping to ‘fall upon’ some sort of insight by the time they’ve finished reading.
If they get to the end and still haven’t had the insight, up goes the hand. “I’m stuck!“
Very quickly the expectation of being stuck becomes a habit, and word problems themselves feel ‘impossible’ before the children have even finished reading.
So – as teachers, how might we best help those children?
I’ve tried a range of things throughout my career, with varying degrees of success. I want to briefly examine them here. Firstly, let’s look at the ‘RUCSAC’ method.
This is a 6-step approach to solving Word Problems. Those of you who have tried RUCSAC in the past will know that it won’t help children who are stuck. (Read, Underline, Choose, Solve, Answer, Check)
Specifically, the 2nd, 3rd and 6th steps are of no use to them. So what else works?
I’ve done a lot of work with Bar Modelling over the years.This has proved to be very successful, but it has its limitations.
Bar Modelling is commonly taught as a discrete topic, meaning that children do not get the chance to develop the vital skill of ‘when would a bar be useful and when would it not?‘
This is important, as while the Bar Model is often the easiest way to tackle word problems, this is not always the case. Leading to: “I’m stuck!”

Even before that, I liked to use a chart with a massive variety of suggestions: work backwards, act it out, use simpler numbers, draw a picture, etc. I’m sure you recognise these and can think of more.
But again, I now realise that this leaves the child with the same dilemma: ‘How do I know which of these strategies to choose?‘ The issue is that we often tend to teach as though the light was already on.
By this I mean that since we know that working backwards will help with a particular problem, we might say “Have you tried the working backwards strategy?’ This is leading the witness, rather than building their reasoning skills.
So over time I’ve begun to suspect that I need a different approach. After some thinking, and a fair bit trial and error, here’s my solution.
It’s called W.O.R.D.S. I know what you’re thinking: oh great, another educational acronym. But bear with me. Here’s how it works.
The image on the right sums up my five suggestions.
Firstly, What is the question actually asking you to do?
‘I am constantly amazed by the children who say “I‘m Stuck!” but who have not even asked themselves this crucial question. The top tip for this is to look at the final sentence before you go back and re-read the whole question. There will either be a question mark to find, or a word such as ‘FIND‘, ‘CALCULATE‘, ‘PROVE‘, ‘EVALUATE‘, ‘SHOW THAT‘ etc.
Any child can do this!
Secondly, what is the One Thing that this question is about? It’s not about the wonderful birthday or the exciting race, it’s probably about candles, pounds, or kilometres. Just one thing. This helps get rid of what I call the ‘net curtains of obscurity‘; the extra ‘stuff’ that’s not relevant to the thing we’re trying to find out about.
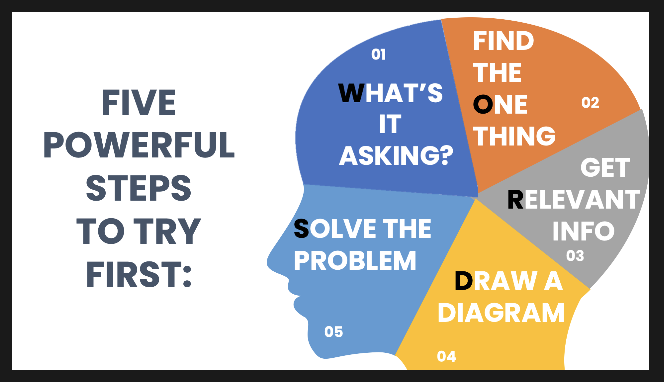
Because of course, once you’ve found out what the question is really about, you are in a much stronger position to sift the Relevant information from the chaff. Anything that doesn’t relate to the ‘One Thing‘ is probably not important. So this helps children focus on just the bits they need at each stage.
Draw a diagram is not new of course, but I have added the advice that this could be in your head. One of the issues with teaching Bar Modelling is that some children find it annoying to have to draw bars, because they can already ‘see’ what calculation is required. That’s fine – the only purpose of a Bar Model is to find the correct calculation. Any diagram or picture that achieves this is fine, drawn or mental.
However hard we try, it’s impossible to avoid having ‘Solve the Problem’ as a final step.
And ‘WORDS‘ has a nice ring about it, don’t you think?!
To check out the exclusive webinar where I go into greater detail about this strategy, click the button below.
You will also receive a free animated PowerPoint Presentation that you can share freely in your school to teach this approach to your pupils.
Let's make "I'm Stuck!" a thing of the past.
* For anyone who for some reason wasn’t able to work it out, the answer was (obviously) ‘Manchester City‘. ;-)
