Part 1 (Monday am). Part 2 (Monday pm). Part 3 (Tuesday am)

After lunch – in which I had great catchups with lots of people – Liz Woodham, Alison Kiddle, and even my former OUP editor Sian Smith which was a wonderful surprise – I headed off to a session I knew would be interesting but not too taxing – Debbie Morgan and Rachel Vincent (Reception teacher at Gamesley Primary School in Derbyshire) talking about the impact of the Mastering Number programme.
For those who don’t know, Mastering Number is an NCETM programme aimed at teachers of Rec, Y1 and Y2. I’m biased, having worked with a couple of workgroups in the Kent and Medway Maths hub on the programme, but I can honestly say that this programme has the potential to have more impact on children’s mathematical attainment than anything I’ve come across since the introduction of the Numicon programme.
We started by looking at Rekenreks. Debbie recommended this free resource for a good learning trajectory with the Rekenrek.
The Mastering Number programme contains five elements:
SUBITISING
CARDINALITY, ORDINALITY AND COUNTING
COMPOSITION, COMPARISON
ADDITION AND SUBTRACTION
Debbie talked about using dot patterns “Is this 7 or not, and how do you know?”, stem sentences (e.g. 9 is made of 6 and 3, and 3 and 6 make 9, building on visualisation of a square)
We watched and discussed videos of children subitising, and solving problems such as 7 = ? + 4 using the part-part-whole structure.
Rachel took over and briefly described her school setting (64% FSM). Children start with very low baselines, and often poor communication and language skills. They introduced the MN programme two years ago, and Rachel said it has had a huge impact on the children. She showed several images with examples of maths in the school.
First – gesture. An important part of the programme, and we saw very short clips of children using gesture to explain their thinking.
Second- stem sentences: Rachel said these had had a massive impact on the children, and it is starting to become natural for children to use stem sentences to explain their thinking.
We spent what felt like ages watching a video of a small group of young children trying to fill gaps in an arrangement of pentominoes – this generated a lot of discussion.
Third – wow moments: Rachel said that some Numberblocks episodes and the use of dice patterns had really helped the children understand key concepts such as doubling. We watched a child building a staircase pattern – i.e. ‘one more’ – with unifix cubes (some of which had been disguised as Numberblocks!)
Sue Gifford who was in the session, talked about how the staircase patterns helped children combine the cardinal and the ordinal – to be honest, this one idea could have been a whole session all on its own.
Back to Debbie – a bit of subitising fun with some fast slides using Hungarian Numberframes, classic tens frames and Rekenrek imagery. Back to the Rekenreks, we put 12 beads on using all ten from the top and 2 from the bottom – Debbie made the point that while there are different ways to show 12, if we want to show that it’s 10 and 2 we should use all ten from the top and three from the bottom.
On to one of my favourite representations the double-decker bus. The image is cleverly designed to mimic the Rekenrek with ten seats upstairs and ten seats downstairs.
Discussions were had about the nature of the programme – it is described as an intervention but is actually for everyone. Debbie said that the Basecamp online community had not been very successful. Someone suggested it could be a Facebook group – in case anyone from NCETM is reading this, I 100% AGREE. The argument that Facebook is not professional enough is a nonsense. I belong to several professional groups online. The reality is that teachers almost all are using Facebook already, and are much more likely to go there to post their thoughts, questions and updates. The current system of using Basecamp just doesn’t work, so let’s be pragmatic and use a forum that teachers will actually use.
Anyway – time for a quick cuppa and then onto the final session of the conference- Colin Foster’s closing plenary entitled ‘Less is More‘. It’s really Colin that you need to blame for this four-part blog; his blogs during his time as MA president have been really inspiring, and provided food-for-thought.
Colin explained his title was a reference to the fact that teachers were facing enormous pressures at the moment, and he felt it was important that nobody left the conference feeling they had a big to-do list, so he would be exploring how to achieve more by doing less.
‘Improving by removing’ – we are hard-wired to solve problems additively, and tend to overlook the possibility of what Colin called subtractive solutions – so what should we do less of? Colin had six suggestions (from least to most controversial)
1: Less Teacher designing from scratch; more adapting of what already exists. Colin’s Mathematics Education Network is designing sets of KS3 resources, hoping to have Y7 Y8 and Y9 in the autumn of 2023. He recommended finding something, trying it, and thinking about how to adapt it. I wondered about the Oak Academy, for example.
Note to self- check it out. I know a couple of brilliant maths-y people who work for Oak (Ed Southall and Emma McCrae) so I am minded to trust their resources, but I’ve never actually looked – my bad.
So – stop planning individual lessons, said Colin, and instead plan a sequence of activities that build together – “Lessons don’t have to be neatly rounded off at the start and end“. Walking out with some unresolved ideas and things to ponder could be very beneficial.
2. Less Crowding of content; more breathing space for sense-making. The easy question is: What are the things that really matter? The harder (but perhaps more important) question would be “What are the things that are of less importance?” As an example, y=mx is for Colin a crucial central idea for KS3 in terms of understanding proportionality, ratio, gradients, scaling, numberlines, multiples and factors, etc. It strikes me that in KS2 there is also potential for using the idea of a multiplier as a relationship between two values.
I’ve not thought about that very much, so it’s certainly a big idea I’ll be chewing over on the train home. Colin added a few other possible areas of impact such as rates, compound units such as speed, or even trig: opposite = tan x adjacent, and so on.
By identifying fewer bigger ideas like this, this could create space for reasoning tasks with little prior knowledge required. Here’s a good example that Colin posed:
Problem: Asim owes Bel £305, Bel owes Chloe £307 and Chloe owes Asim £100. What is the easiest way for them to settle up?
‘No Priors’ tasks have a levelling effect, explained Colin. Everyone has to think, anyone can shine, anyone can learn from anyone, and anyone can devise a problem that everyone else will find challenging.
3. Less Rote Memory, more making connections. Colin gave the example of learning multiplication tables – knowing a few key ones and focussing on how to build on them to find others frees up the mind. He posed another rhetorical question: is it better to work it out really really quickly or recall it instantly from memory?
Nice trick to multiply teens: 14 x 18:
- 4+8 = 12 (then multiply by 10 to get 120)
- Add 100 (220)
- Add 4 x 8 (252)
4. Less Calculating, More estimating: for example, the QAMA calculator refuses to give you an answer until you give it a reasonable estimate! Often an estimate is good enough, after all!
I was too slow to catch a show of the first example but the second was:
Which is less, 6×8 or 7×7? 16×18 or 17 x 17? 1116 x 1118 or 1117 x 1117?
What about 36 x 48 or 38 x 46? Colin put up a series of slides in rapid succession with the same question, but with ever-deepening areas of maths.
x+3 = 10, x+3 = 3, x+10=3, 2x+3 = 10, x2= 10 and so on – to solve these you need to accept the existence of more and more numbers!
We then thought about ‘i‘ as the square root of negative 1…where does it sit on a number line? Turns out – it doesn’t. Much laughter ensued at the apparent contradictions that this brought up. Here’s one of the slides, where Colin showed us a way to think about it:
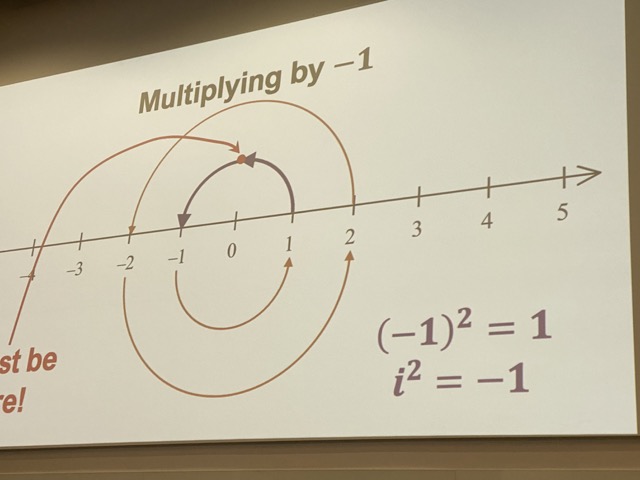
5. Fewer different representations, models and examples, and more depth: Every new representation brings with it a time cost.
As a quite brilliant closing thought, Colin said that although we thought there would be six points – there were actually only five. Because – less is more!
He then challenged us to change something – by doing less. I’ll give that some thought on the train back to Brighton tonight.
Tom Roper thanked Colin and then opened the floor to questions (or for people to make short soapbox speeches designed as questions, you know the drill).
Ok, that’s more than enough – I hope you’ve enjoyed this series of blogs from Warwick; time to shut the laptop and head back home. What a terrific maths conference. Massive thanks must go to the amazing Karens, Alice, Jane, and their hard-working teams of peeps doing so much behind the scenes.
I also think we should take time to reflect on what an emotional time this must have been for the MA and ATM staff; they are inevitably looking to the future, and wondering a) whether this was their last conference as staff of their respective associations, and b) what role they will have if and when we form a new single association; so whatever the outcome of the ongoing discussions, I really hope everyone continues to appreciate their valuable work in supporting us over the years, and making these fabulous conferences happen.
On a personal note, I don’t think I’ve ever had so many meaningful conversations with so many people in one 48-hour period before. Old friends, people I knew a bit from the maths world, people I only knew by name or reputation – without exception I enjoyed every single interaction. And to unexpectedly see my former editor Sian, with whom I worked for over two years on the Numicon Handbooks, was the absolute icing on the cake!
This is also the first time in over 20 years that I have attended every single session of the conference without taking time out, so that’s a testament to my ADHD meds, I guess :-)
Enough. It’s wine o’clock.
