I’ve been experimenting with something I’m calling ‘Gateway Questions‘ this morning. This has come about because I am working with a KS2 class who have a huge ability range, perhaps as much as the equivalent of 4 NC years.
This is not unusual in many classrooms, sadly. The truth is that a ‘whole-class’ Mastery approach is neither appropriate nor viable in such classes. Fortunately we are in a position where there are plenty of adults to support the teacher, so smaller groups is a common feature, even if only for part of the lesson.
For the avoidance of doubt, I am strongly in favour of teaching the class as a whole class whenever possible. But it is important to acknowledge that there are times when it is not in the best interest of some children.
There is a danger with groups, of course – children can become used to being a ‘top set’ or ‘bottom set’ mathematician, and begin to develop unfair and unnecessary expectations and beliefs about themselves and their ability. This is why quite rightly many teachers keep their groups fluid, and acknowledge that some children are better at some aspects of maths than others.
But anyone who has tried this will know that even this method is far from perfect. Sometimes a child simply cannot grasp something, despite the most expert of input, while another turns out to have been working way below their ability.
Enter the Gateway Questions. At the start of the lesson, I put up two or three carefully designed questions. The first covered the simplest example of what was done in class the previous day, the second was an example of the hardest thing that was covered, and the third was a tiny bit beyond what was explicitly taught.
The whole class have a go at these at the start of the lesson. Their answers provide all the information required to make an accurate assessment of who would be best served in which group. This approach seems to me to offer great benefits:
- Recapping previous work helps to embed it in long-term memory
- Everyone gets straight to work early rather than waiting for the ‘your turn’ bit.
- Teachers can get a very quick assessment of how much of yesterday was understood, rather than just superficially remembered in the moment.
- The class can be split into groups based on what they need right now, rather than pre-conceived ideas of what they can or cannot do.
- Nobody needs to think of themselves as a ‘higher’ or ‘lower’; they are just mathematicians.
- The teacher models the three answers before splitting up the class, so everyone knows what will be coming next.
This morning’s gateway questions were to find 484 ÷ 4, 504 ÷ 4, and 504 ÷ 3.
We had prepared for this by exploring various methods with them the previous week: PV counters, part-whole models, bar models, Dienes, etc. We walked round and looked at who could do which questions on their whiteboards.
Almost everyone could do the first, about half the class could do the second and about three children or four could do the third. On this basis it was easy to decide how best to split the class – those who were able to do the second question formed one group and the other group stayed to learn how to cope when one of the digits in the dividend was not an exact multiple of the divisor.
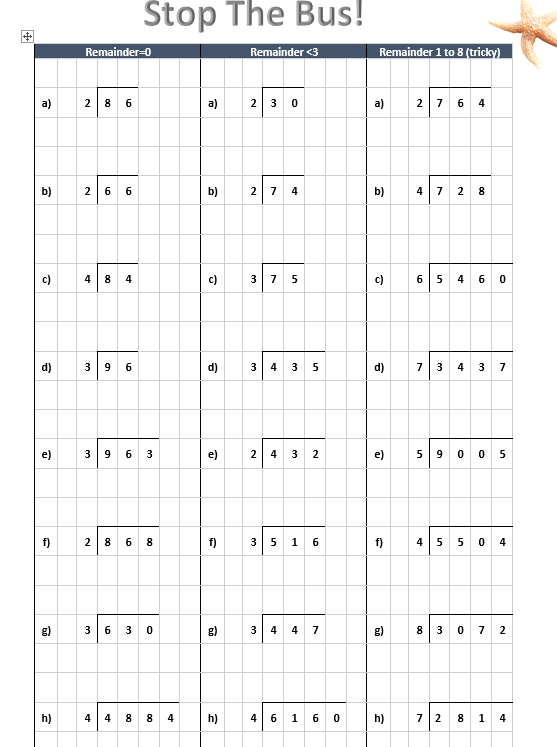
Pre-prepared based on the children’s progress the day before, was this ‘Stop The Bus’ worksheet. Take a look at the careful variation included between the three sets of questions, and within each set…
The children who could not do the second gateway question stayed in class, reviewed previous work and worked on the first two columns.
The other children came to a next-door classroom and started with the second column, progressing to the third. Those who had not been able to do the third gateway question all came next-door, and were given extra support before going onto the third column, where the ‘carries’ were not restricted to either 1 or 2 and the divisors were potentially as large as 9.
This worked well – both groups made good progress at an appropriate level of challenge, (ZPD fans take note!) without wasting a lot of time. I’ll definitely be exploring this idea further.
N.B. Obviously halving a class is not always an option, but this method could also be employed equally effectively to choose groups to work with a TA, for example. That avoids the ‘I’m in the special group’ mentality.