Click here for part 1 (Monday morning)

Following a beige lunch (but on real plates, so hey) I headed to the first session of the afternoon, led by Carol Handyside and Louise Langford. Just to reassure you, I didn’t know either of them, but they clearly knew their stuff.
The session was entitled “Well-Chosen Manipulatives to develop a Deep Sense of Number‘. Their opening challenge was to work out what 5 + 4 + 8 was, but more importantly how did we think about it.
We spent a while talking about the various strategies (partitioning the 8, etc) but what really interested me was how long it would take to get children to choose to use an efficient method.
There is a gap between concrete and abstract thinking – I think we don’t talk about that enough. It’s tempting with a group of teachers to say ‘I just split the … into… and … and put the … with the …’ but for me the BIG challenge is “How do we encourage and support children to move from the written question to the answer via the most appropriate use of manipulatives.
I did like Louise’s assertion that it doesn’t matter which manipulative you use as long as it scaffolds your thinking. After all, I think the paradoxical purpose of any manipulative is to make itself redundant; but how can I be sure that by giving children manipulatives, they will in future use what they noticed when talking similar problems. I still don’t have an answer, which may explain why this sort of practice is not more prevalent.
Our group (Helen, Caroline, me) tried counters on Hungarian tens-frames, and there was an interesting moment when Caroline moved a single counter allowing me to see the addition in a very different way, so it’s not that I need convincing about the use of manipulatives; it just made me want to know more about how we as teachers decide when to remove or reduce access to them.
Butterworth (2019) suggests that we can only subitise up to 4, so linear imagery is less useful than cluster images such as Numicon, Hungarian Tens Frames, Bead Strings, etc.
Louise questioned whether children recognised dice patterns as much as they used to – she did recommend them as visual images of numbers. They are a good way to visualise doubles, for example.
Next we looked at this image and talked about how it might support our thinking around adding 7 and 7.
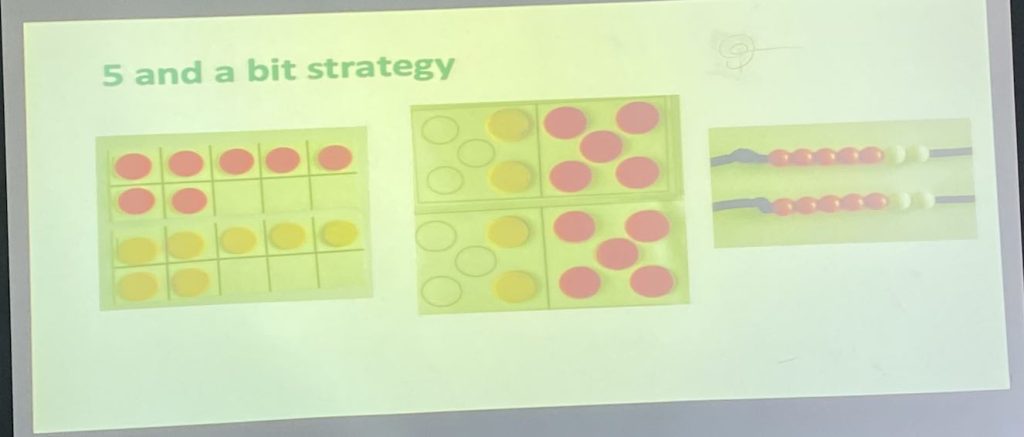
Lots of interesting discussion ensued. Which of these images encourages children to think of this as 5+5+2+2, for example, and which use ‘negative space’ to see that it’s 20-6. One delegate was really struck by how the way in which we arrange our manipulatives has a big impact on the strategy we choose.
Another said that they felt a beadstring would support children whose counting was weak. I found the discussion around the two different tens frames very interesting – one delegate questioned which one might make it easier to subitise the ‘5’.
The ‘curse of expertise’ was mentioned, and I think this is VERY important. We must be vey careful about the idea of using a manipulative to represent more than one thing, or at least about assuming that children can be as flexible in their definitions as we can be. I was shown this report, which suggests that we may do more harm than good by redefining the value of a manipulative.
Both Carol and Louise had some interesting thoughts on what the barriers might be – I think this is something I need to think more about – for example, which tens frame is better, for what, and why?
I headed down a mental rabbit hole thinking about this – the whole point of, for example, Cuisenaire, is that each rod can and should represent DIFFERENT amounts – their value only has meaning relative to another rod. And I’ve had success with using Dienes 100’s to represent 1’s when talking about decimals. But maybe I need to rethink this.
To me the crucial thing with decimals is that the idea of place value is not about what each column is worth, but rather what it is worth compared to the columns to it’s left (a tenth of it) and its right (ten times it). The fact that this is true whichever base 10 column we are in seems to to me to be the fundamental truth at the heart of place value. The decimal point makes NO difference to the structure – none.
Meghan Trainer was right – it’s ALL about the base.
No sooner had I finished writing that sentence, than Louise put a Mahesh Sharma Cuisenaire idea under the visualiser. Actually I wondered whether Gattegno might have done it first, and very likely Madeleine Goutard (1964). It was five ‘whites’ in a dice pattern, then in a row…add a yellow to show the length is equivalent…then find all pairs to make 5, etc. All linking to the ‘part-whole bar model’ (see Bar Modelling in Key Stage 1, Jeffrey, 2018)
Next group task: explore number facts for 18. Confession; our table didn’t. Not because of our naturally subversive tendencies, but because Caroline is doing some advanced research in this area and she, Helen and I got into a fascinating debate about the use of two-colour counters and negative numbers. I felt a bit bad because I know we were going somewhat beyond the remit of the session, but Carol and Louise were very patient with us!
Final Reflections: Louise shared some research (Benz, 2014) ‘Identifying Quantities of representations’. This was a good place to finish – flexible partitioning is the thing that feels most likely to impact children’s ability to move from counting to calculating. Carol also reminded is about Equals magazine which is freely available from here.
Fascinating – the old brain hurts now, so I might skip the next session. Even though I took my ADHD meds this morning I am really struggling now with concentration. I really hope this is at least partially coherent!
Actually, hold that thought – I’m co-writing a book with Liz Gibbs about mental maths at the moment (publishers feel free to get in touch!) so I thought I’d go to another double-act session: Anthony Reddy and Dave Godfrey’s session called ‘Time to Reimagine Mental Mathematics in the Primary Classroom‘. ‘Not that Dave Godfrey?’, I hear you ask. Yup – the original Mr Number Fun himself :-)
Anthony is a former National Strategies consultant who describes himself as having spent the last 20 years living on the M6 – the National Strategies had much better guidance on mental arithmetic, while the 2014 Curriculum intentionally or otherwise relegated them to appear far less important than formal written algorithms.
He started by writing up 45+29, 637+198, 5367+2996, 4.5+2.9 and 6.37+1.98 and asking how we would do them. Unsurprisingly he said that 95% of children would jump straight into columns, without spotting how easy they would be if we had a more developed ‘Number Sense’.
Someone mentioned Jo Boaler’s YouCubed website which also encourages this. Anthony talked about his new M.A.P. (Mental Arithmetic Practice) system.
Three main elements: counting skills, learning of key facts, mental strategies.
Can children count on in fours – from an odd number? Anthony suggested they can’t.
We had a discussion about 45+29. Two main methods – transfer one of the 45 to the 29 giving us 44+30, or do 44+30 and subtract 1.
It reminds me of a lesson in the last year in which I asked a Y6 child the following question: If 46+73 is 119, what is 119 -73? He had no idea. And another did 9 + 7 but starting with 9 and counting on 7 more to 16.
Naively, perhaps, I found this staggering. The conatersation started me thinking that we need to get back to a more flexible approach to mental arithmetic. Back to the session…
I began to think that Anthony and Dave were pitching their M.A.P scheme. This is not in any way to criticise them, as I think they have identified a vital need. And actually they have addressed it so well that I didn’t mind being pitched to!
Dave put up a slide from the NC showing that ‘the principle focus in lower KS2 is to ensure that pupils become increasingly fluent with whole numbers and the four operations including number facts and the concept of place value.’ He asked us what strategies we might choose for 25+28.
Our answers were similar to the previous question, with the most notable additions being doubling 25 and adding 3, or doing 25+20+8…
I enjoyed Dave’s use of a giant abacus to clearly show counting on, from any number, in a range of multiples…
Time for a game: Anthony asked us to roll a 1-20 dice. If it’s even, half it. Next player’s turn. If it’s odd, add 19. Next player’s turn. Win a point if you get back to the number rolled. Loved that! I’m definitely going to include it in the April newsletter…
Dave showed a slide with the 2010 ‘Teaching Children to Calculate Mentally’ document from the DfE. It’s still available online from here and is a blast from the past but with hidden gems – check it out.
It has details of all the key strategies, including manipulating, rounding and adjusting, partitioning, counting on, double adjust etc.
It made me reflect on why as a profession we seem so terrible at throwing out the baby with the bathwater.
Next came a treat- a song about a parrot helping two pirates, one who had 38 coins and one who had 13 coins. I realise that this is a bit of a cop-out, but ‘you had to be there’.
Dave has developed the parrot (which he described as a influencer after a teacher told him that all her kids were copying the parrot’s method) and added more characters (Papa Titionin), Jumping Kangaroo, the Doubling Twins) all of whom have different strategies. We went back to 25+28 and asked what each character might do. This is really clever as it forces children to try to understand how to apply the different strategies. I leave the answers as an exercise for the reader, naturally :-)
Finally Dave and Anthony did talk about three ways in which such an approach might be timetabled, but I wasn’t really able to focus to be honest as my ADHD brain is pretty much shot again. I’m so glad I decided to stay on and attend this excellent session. Need a bit of a kip or a walk now, I think…
Will add some further thoughts later…
